我家狗子引发的一场“惨案”，竟讲清楚了傅里叶变换……

上了一天班，小编拖着疲惫的身体打开家门，却看到了这样的场景：

①餐桌上的火腿被吃了；②沙发被抓破了；③床上有一堆shit。

小编找到自家的狗砸，看着它无辜可爱的大眼睛，以及天使般的笑容，心里一软，“来，我给你个痛快的。”

狗砸这时急得说出了人话：“你莫要冤枉好狗，有什么证据证明这些事情都是我做的？如果是我，我的作案时间是什么？本着疑罪从无的原则，证据链不完整我可不认。”

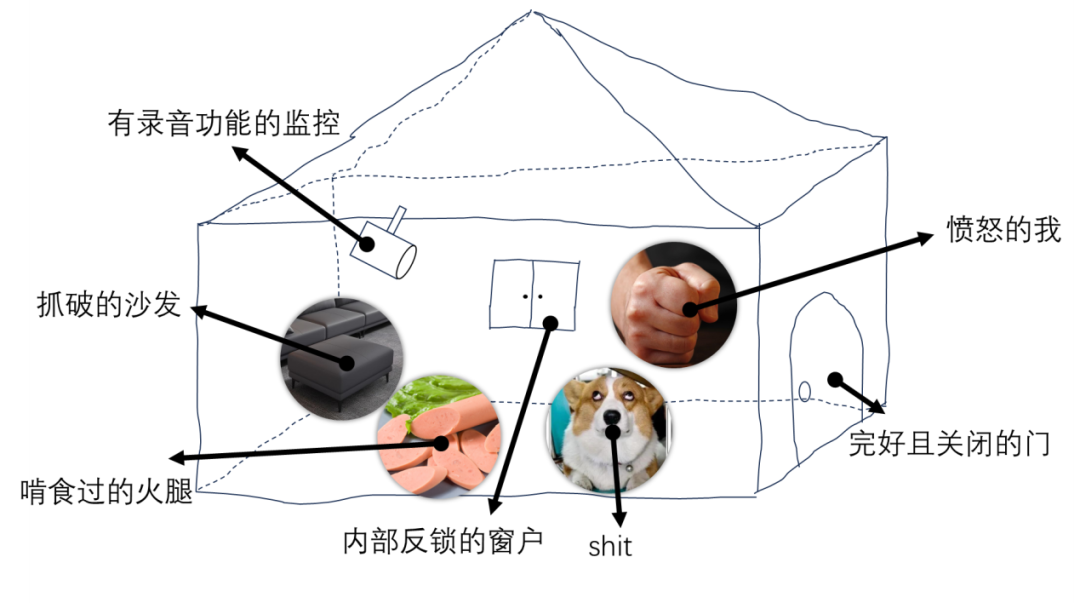
案发第一现场的示意图

等小编翻看监控，却发现这条狗砸全天避开了家里所有的摄像头，只录到了它的声音。小编不甘心让它逃脱制裁，决定求助于一种工具：傅里叶变换。

简单来说，我要做的事包括：

①判断当天发生了什么犯罪行为；

②确定犯罪行为的发生时间；

③在狗砸面前还原完整的犯罪场景。

而小编手头的证据只有当天家里的录音，那么破案就从这里开始。

生物的每种行为都有独特的频率特征，例如唱高音就是发出高频声音，唱低音就是发出低频声音。假设我已知狗砸“吃火腿”、“抓沙发”和“shit”的频率特征，那么只需判断家里的录音是否包含对应的频率特征，即可识别出犯罪行为。

为此，我们需要将录音的时域信号 f(t) 转换为频域信号 F(ω)，这个转换依靠一个特殊的公式：

傅里叶变换的公式

这个公式要怎么理解呢？这里给你个最通俗易懂的解释，保证一个公式都没有：

你的面前有一堆砂子，里面混有不同种类的矿石，现在需要你给出每一种矿石的量。恰好，你手里有多种磁石，每种磁石只能吸附铁、铜或铝等特定物质。

你只需依次用每种磁石在砂堆里滚一遍，磁石就能将对应的物质提取出来。上述过程将一堆砂子转换为不同的物质成分，且能够确定每种物质成分的量。

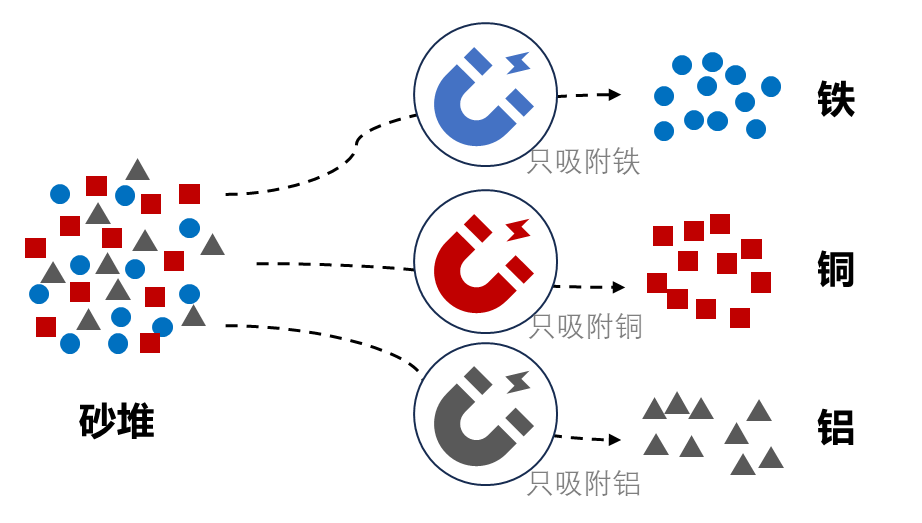
利用磁石提取物质成分

类似地，傅里叶变换公式中的e^-jωt就是“磁石”，它能够“吸附”频率为ω的信号，而对时间积分就是“在砂堆里滚一遍”，确保提取出所有频率为ω的信号数据，即为F(ω)。

最终，傅里叶变换将时域的信号转换为不同的频率成分，且能够确定每种频率成分的“量”。

举例来讲，大大布和小小二一起唱歌，大大布发出ω=50的低音，小小二发出ω=100的高音，我们能用e^-j50t提取出大大布的低音，用e^-j100t提取出小小二的高音。

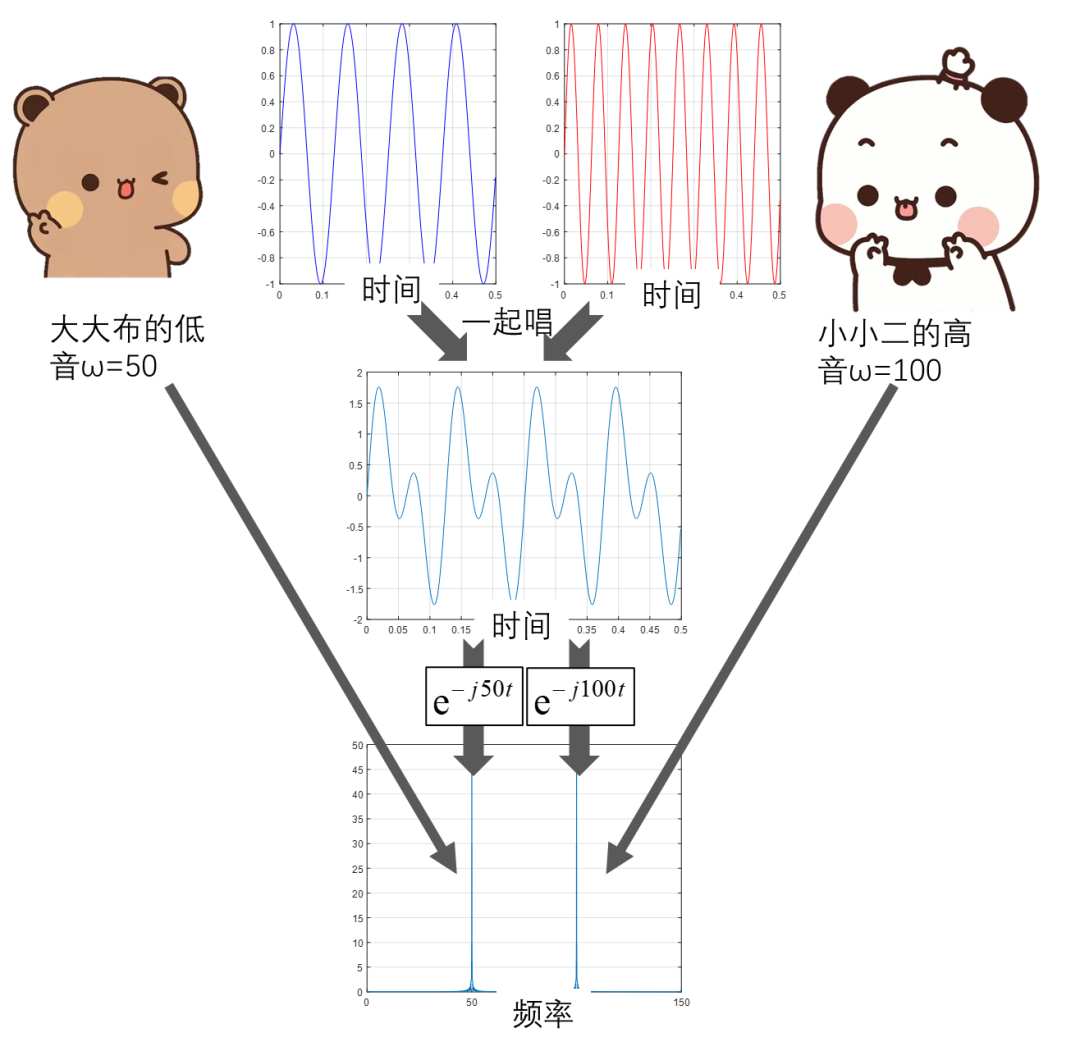
好了，傅里叶变换已经解释完了，你就说是不是一个公式都没有！

现在让我们根据傅里叶变换的原理来识别狗砸的犯罪行为。已知“吃火腿”、“抓沙发”和“shit”有不同的频率特征，我们用傅里叶变换将录音转换至频域，如果发现了相应的频率特征，就能断定今日发生了上面三件骇人听闻的犯罪行为。

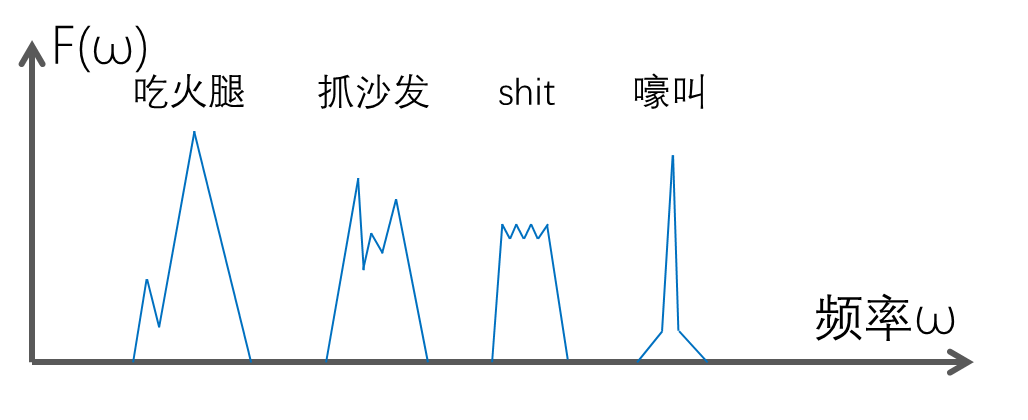
根据频率特征确定犯罪行为

（记住这个“嚎叫”，后面用得上）

仅识别出今日发生的犯罪行为还不够，我们需要确定各行为发生的时间。这时，我们发现一个问题：傅里叶变换将时域信号转换至频域，却也抹除了时间信息。

回忆砂堆的案例，磁石将不同物质成分提取出来，我们也就无法判断各成分的空间分布，例如铁在砂堆中的分布位置。类似地，傅里叶变换把不同的频率成分提取出来，我们也就无法判断各频率成分的时间分布。

举例来讲，大大布和小小二一起唱歌，但大大布在5~20秒内唱，小小二在10~30秒内唱。当把歌声转换为ω=50和ω=100两种成分，我们也就无法区分他们唱歌的时序。

为解决傅里叶变换的时间信息丢失问题，有人提出了一种有趣的方法——短时傅里叶变换。

还是唱歌的例子，我们将歌声分割为多个时长为5秒的片段，对每个片段的歌声进行傅里叶变换，发现0~5秒内没有任何频率成分，5~10秒内只有大大布的频率，10~20秒内有两个人的频率，20~30秒内只有小小二的频率。这样一来，我们就能判断出大大布大致在5~20秒内唱歌，而小小二大致在10~30秒内唱歌。

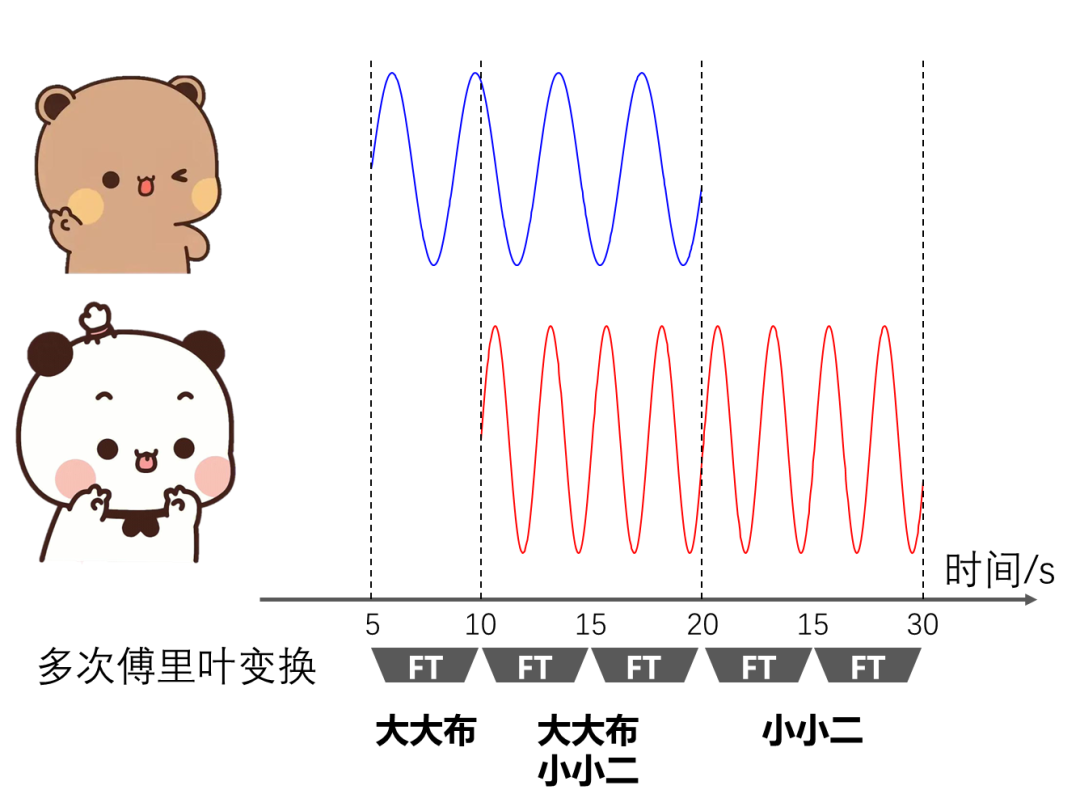
短时傅里叶变换的原理

类似地，我们把案件现场的录音分割为多个10分钟的片段，对每个片段进行傅里叶变换，在10:00~10:10发现“吃火腿”的频率，在12:00~12:10发现“抓沙发”的频率，在15:00~15:10发现“shit”的频率。这样一来，我们就大致确定了三种犯罪行为发生的时间。

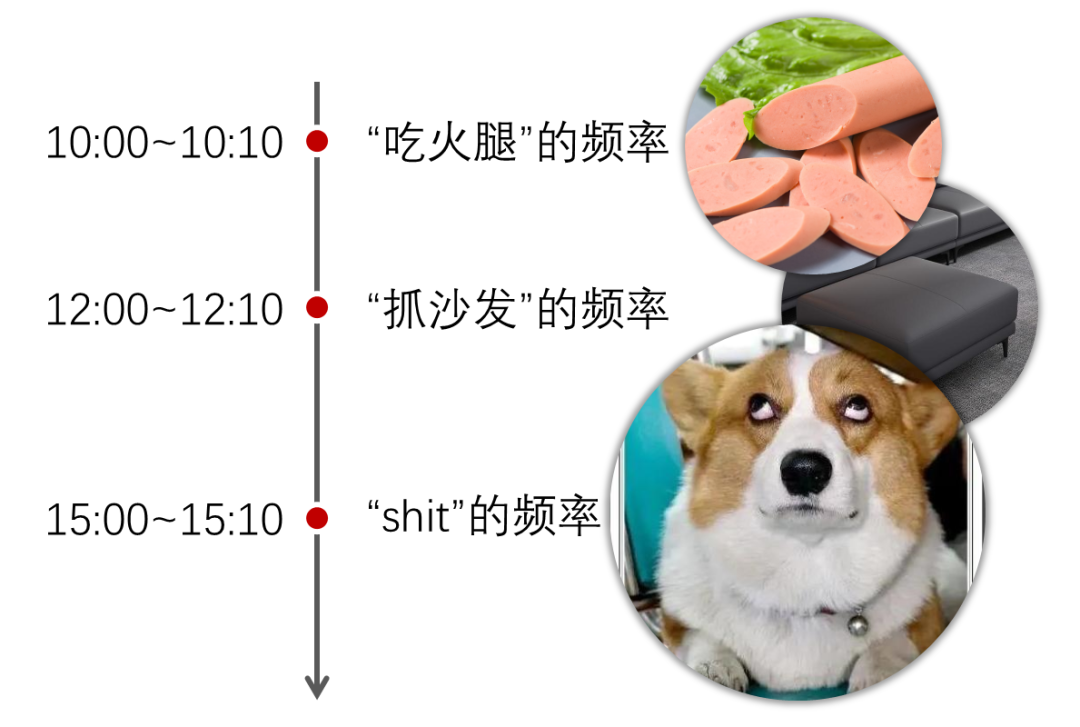
通过短时傅里叶变换确定犯罪时间

短时傅里叶变换就是一种联合时频域的分析方法，即保留了时间信息，又具备将时域信号转至频域的能力。

不过注意，时段的长度不能太长，也不能太短。时段太长会导致时间分辨率较低，例如我们现在只能确定狗砸在10:00~10:10吃火腿，但无法确定具体哪一分钟。而时段太短又会导致频率分辨率较低，例如10秒的时段会录不全“吃火腿”的声音，进而导致算出的频率有误。

总之，在傅里叶变换中，类似于量子力学的测不准原理，时间分辨率和频率分辨率不可兼得。

识别出犯罪行为和确定犯罪时间还不够，我们还需要在狗砸面前还原出完整的犯罪现场。本来，我们已找到各犯罪行为的时段，只要调取相应的录音即可。然而我们发现，在15:00~15:10，狗砸竟然边嚎叫边shit，两种声音混杂在一起。这时，我们求助于频域滤波和反傅里叶变换。

狗砸的特殊习惯，便于发力

依旧拿砂堆举例：若我们想要不含铁的砂堆，那么可以这样做：

①移除吸附铁的磁石，只保留吸附了铜和铝的磁石；

②关闭磁石的磁性，将此前吸附的铜和铝混合在一起。

这样一来，我们就得到了不含铁的砂堆。

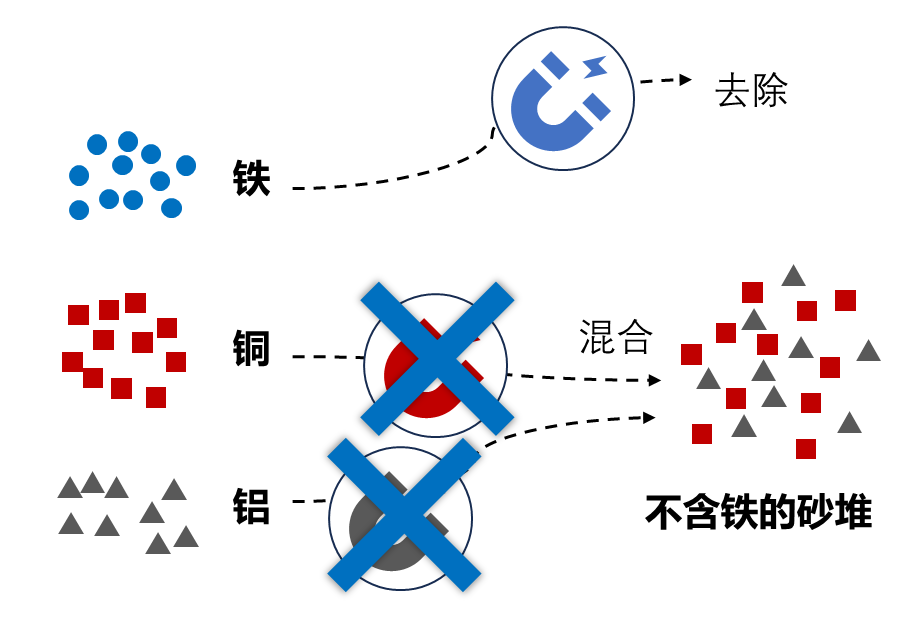
剔除砂堆中某种物质成分的方法

频域滤波：类似地，若想还原出狗砸“shit”的音频，我们可以构造一个只允许“shit”频率通过的设备，让“嚎叫”等其它频率成分清零。这个过程被称为频域滤波，相当于步骤①（只保留特定的物质成分）。

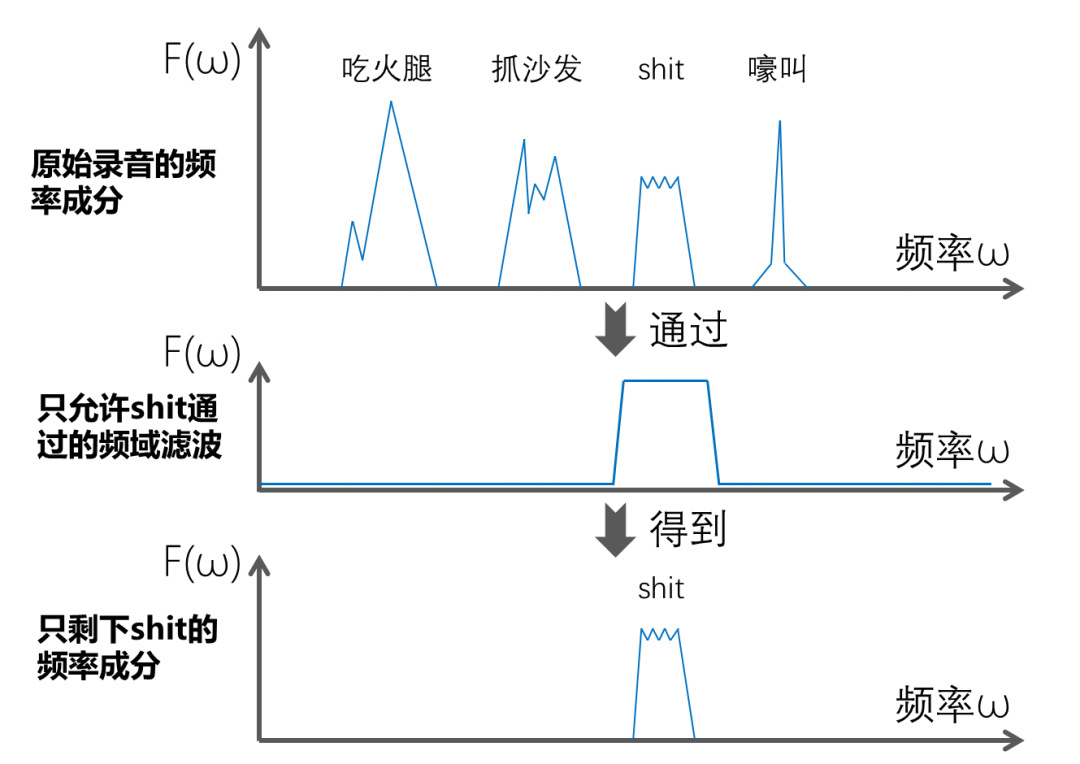
剔除某种频率成分的方法

傅里叶逆变换：紧接着，我们利用傅里叶逆变换，将频域信号还原至时域，相当于步骤②（关闭磁性，并混合成分）。

傅里叶逆变换的公式

相比之下，傅里叶变换的e^-jωt类似于磁石的吸附能力，傅里叶逆变换的e^jωt就是“关闭”这一吸附能力，而对频率积分相当于将各种频率成分混合在一起。

傅里叶变换与傅里叶逆变换的对比

如此一来，我们就可剔除15:00~15:10录音中的嚎叫声，还原出“shit”的录音。对于其他时段的录音，我们也可用频域滤波剔除可能出现的噪声（远处的施工声、窗外的鸣笛等），更好地还原出犯罪行为的录音。

至此，我们便根据今日的录音识别出狗砸的犯罪行为、确定了犯罪时间、并还原出犯罪场景的录音。当然，最重要的是，带大家学习了傅里叶变换！

傅里叶变换不只是一种数学工具，它早已应用于生活和工作的方方面面，举例来讲：

（1）手机的音乐识别：每首歌都有独特的频率特征（类似于歌曲的“指纹”），通过傅里叶变换将歌曲片段转换至频域，就能从数据库中匹配出最相似的歌曲。

（2）机器的无损检测：正常工作的机器和故障/即将故障的机器发出的频率是不同的，我们可以对机器声音进行频域分析，从而在不打开/破坏机器的前提下，检测出机器的故障原因，甚至预测机器何时发生故障。

（3）电脑的图片优化：一幅图片中缓慢变化的部分对应低频信号，例如绵延的草原；而急剧变化的部分对应高频信号，例如人的边缘。傅里叶变换将图片转换至频域，滤除高频信号就是图片模糊，而滤除低频信号就是边缘锐化（某图秀秀的用户一定很熟悉这两个功能吧）。

（4）金融的时序分析：金融数据非常复杂，是一种典型的非平稳信号（别问，问就是下期再慢慢解释），但傅里叶变换依旧能从中提取出周期性的成分，以辅助人们进行金融决策。

傅里叶变换的应用案例

好了，不多说了，跟大家讲完傅里叶变换，我也要给我家狗砸上课去了！